Océanographie des astronomes
Bruno Voituriez.
S’il est un mouvement de la mer facilement décelable, c’est celui des marées dans les régions littorales ; du moins dans les aires océaniques, car la marée se fait nettement plus discrète dans les mers fermées comme la Méditerranée où le niveau de la mer dépend beaucoup plus des conditions météorologiques (pression atmosphérique, vent) et de la morphologie des bassins que de l’attraction de la Lune et du Soleil. En moyenne, l’amplitude n’y dépasse pas 40 cm sauf au fond de la mer adriatique où la conjonction, en automne et en hiver, de fortes marées et des conditions météorologiques particulières peut provoquer des élévations de 1,4 mètres à Venise qui se trouve alors inondée (les fameuses « acqua alta ») et en Tunisie dans le Golfe de Gabès où l’amplitude peut atteindre 2,3 mètres.
On est loin des grandes marées de 13 mètres au Mont Saint-Michel ou de 15 mètres en baie de Fundy au Canada.
Au large, par grande profondeur l’amplitude de la marée ne dépasse pas quelques dizaines de centimètres et passe totalement inaperçue des navigateurs, d’autant que sa longueur d’onde est de quelques milliers de kilomètres. Paradoxalement, il est probable que cette faiblesse de la marée en Méditerranée explique que ce soient les Grecs qui, semble-t-il, se sont intéressés les premiers aux causes de ce phénomène qui pour eux fut alors une découverte, alors qu’ailleurs c’était un état de fait.
Hérodote, ce grand voyageur du 5e siècle avant Jésus-Christ, fait état de ses observations de l'élévation et de l'abaissement journalier des eaux de la mer Rouge. Le phénomène n’était donc pas totalement ignoré des Grecs, ce qui n’empêcha pas les marins de la flotte d’Alexandre à la conquête de l’Inde vers 325 avant J.C., d’être terrorisés par la vision de leurs navires échoués à marée basse.
Au même moment, Pythéas astronome de Massalia, sans doute financé par les commerçants de la ville à la recherche des sources d’ambre et d’étain, part pour une expédition de plusieurs années dans l’Atlantique nord.
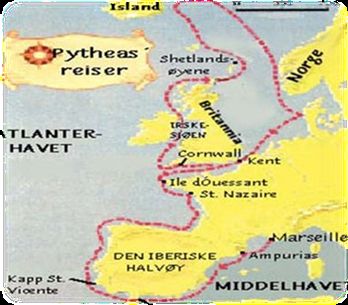
Circuit de l'expédition de Phytéas dans l'Atlantique Nord. Source Blog Dan histoire
C’est la première expédition maritime et scientifique et l’on peut décerner à Pythéas le brevet de premier océanographe de l’histoire, ne serait-ce que pour le titre de son ouvrage qui raconte son voyage : «De l’Océan» dont il ne reste malheureusement que quelques fragments cités par des géographes qui lui ont succédé (Strabon, Eratosthène, Diodore de Sicile, Polybe, Pline l’ancien).
Au départ, la route suivie par Pythéas dans l’Atlantique de Gibraltar à Ouessant et à la Bretagne, puis la Grande Bretagne, n’était pas nouvelle : les Carthaginois et leurs filiales en Espagne l’empruntaient pour le commerce. L’originalité de Pythéas, en astronome curieux, est de poursuivre vers le nord en contournant la Grande Bretagne à la recherche du cercle polaire, pour vérifier l’exactitude de l’inclinaison de l’axe de rotation de la Terre . Il découvre l’Ultima Thulé (Islande) , il atteint au nord de l’île le cercle polaire , voit le soleil de minuit et atteint la banquise. On ne sait trop si, à la recherche de l’ambre, il entra dans la Baltique. Sans doute renseigné par les populations rencontrées (il connaissait le Celte), il constata non seulement qu'il y avait deux pleines et basses mers par jour lunaire, mais également que l'amplitude de la marée dépendait des phases de la Lune. Pythéas n’est certes pas l’inventeur de la relation entre les astres et la marée.
Héraclide (388-315 Av.J.C.) peu avant lui, avait déjà avancé cette idée, mais c‘est incontestablement lui qui fut à l’origine de l’approche scientifique des recherches sur la théorie des marées. Quelques siècles plus tard, Pline l’Ancien (V.23 79 après J.C) dans son «Histoire Naturelle» décrit très correctement la marée en la liant à la lune et au soleil sans faire d’hypothèses sur la nature des causes de cette attraction à distance entre les astres.
L’explication qui eut cours, le plus souvent à partir d’Aristote, fut le principe de «sympathie» : l’eau de la Lune attire l’eau de la Terre. C’est encore l’explication avancée par Képler (1571- 1630). Galilée, en difficulté pour faire admettre la rotation de la Terre sur elle-même et autour du Soleil, élimine le Soleil et la Lune, et tient un raisonnement qui relève du sophisme. Les marées, dit-il, sont dues à la rotation de la Terre sur elle-même ; comme les marées existent, nécessairement, la Terre tourne sur elle-même. D’autres explications eurent cours au Moyen-âge : le heurt entre les courants océaniques déjà proposé par Flavius Macrobe écrivain latin (370-430). Reprenant l’idée de Platon, Paul Diacre (720-778) pense que les marées ont pour cause un gouffre très profond voisin des côtes norvégiennes, qui alternativement absorbe et vomit les flots. Cette idée vient de l’observation effective de tourbillons liés aux courants de marée du côté des îles Lofoten en Norvège. Tourbillons, certes violents, mais qui n’ont rien d’«aspirateurs». C’est le maelstrom qui inspirera Edgar Poe et Jules Verne.
Un savant arabe Zakariya al-Qwazwini (1203-1283) tenta la première explication scientifique. Selon lui, la marée montante est due à l'expansion thermique de l'eau échauffée par la Lune et le Soleil.
Saint Thomas d’Aquin, qui avait lu Averroès se méfiait de cette idée de sympathie et des qualités que l’on attribuait aux corps pour expliquer les choses, affirma, lui, que sans le secours d’aucune vertu particulière, la Lune appliquait aux eaux de mer une force motrice.
Ce ne fut pas du tout le point de vue de Descartes qui, suivant Aristote et son fameux «La nature a horreur du vide», écarte toute idée de vide et d’actions et de force à distance. Il remplit donc l’univers d’une substance animée, «la matière du ciel», organisée en tourbillons qui transmettent, de proche en proche, les mouvements. Ainsi explique-t-il le mouvement des planètes emportées par de vastes tourbillons de cette matière du ciel.
Pour Descartes, la pression exercée par le tourbillon de la Lune sur celui de la Terre est transmise à la surface de la Terre et génére les marées. Il y avait un souci de rationalisme dans la vision de Descartes qui récusait toute idée d’action d’une force occulte analogue à la sympathie entre les corps. Pour y échapper, au prétexte que le vide ne pouvait avoir d’extension, il conclut que l’espace était nécessairement rempli de matière tourbillonnante.
Newton : le modèle statique
Enfin, Newton vint pourrait-on dire. Il va donner corps à cette force motrice des marées à partir de la «gravitation» qu’il définit dans son ouvrage «Principia» (1687) :
«Les corps s’attirent par une force proportionnelle à leurs masses et inversement proportionnelle au carré de la distance qui les sépare».
Newton justifia cette hypothèse de la gravitation universelle en retrouvant, notamment par le calcul, les trois «lois de Kepler» (énoncées entre1609 et 1619) sur les mouvements des planètes du système solaire, mouvements bien définis par les nombreuses observations très précises de Tycho Brahé (dont Johannes Kepler était l’assistant).
C’est en étudiant les «variations» des mouvements de la Lune de part et d’autre de son orbite moyenne autour de la Terre, que Newton eu le génie d’appliquer la même démarche heuristique pour expliquer le phénomène des marées sur notre globe. Newton a considéré les particules d’eau océaniques, non pas comme un satellite libre tournant autour d’une Terre «océane», mais comme un fluide canalisé selon les lignes de forces génératrices de marée, permettant à l’ensemble de l’eau de circuler dans le canal.
Ayant démontré que la force «variationnelle» était la différence des forces d’attraction du Soleil aux centres des masses de la Lune et de la Terre, Newton définit ainsi la force génératrice de la marée en un point de la surface du globe comme étant la différence des forces d’attraction de la Lune en ce point et au centre de masse de la Terre.
La différence de ces deux forces - chacune proportionnelle à l’inverse des carrés de 2 distances très proches : Lune-centre Terre (R) et Lune-Surface de la Terre (R+x ; x variant de -r à +r avec rayon de la Terre r<<R) - est proportionnelle à l’inverse du cube de la distance Terre-Lune en première approximation. Cette force génératrice est très faible. Elle est de l’ordre du dixième de millionième (1/107) de la gravité terrestre (10 m/s2), soit au maximum de l’ordre du micromètre/s2.
Pour avoir une image plus actualisée, cette force génératrice de marée lunaire est la même que celle qui perturbe l’orbite moyenne de tout satellite artificiel S évoluant autour de notre Planète bleue (voir image Wikipédia).
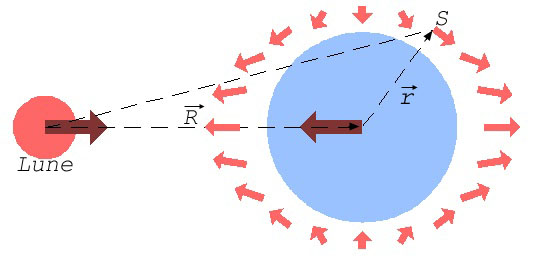
Image Wikipédia : La force de marée induite par la Lune, qui agit sur le mouvement relatif d'un satellite artificiel S par rapport à la Terre est représentée en rouge en direction et en intensité par les flèches. Notons la symétrie par rapport au centre de la Terre. Cette force est très petite par rapport à l’attraction de la Terre proprement dite sur le satellite (de l’ordre du micromètre/s2 comme écrit dans le corps du texte), mais elle a quand même un effet observable, comme on le sait aujourd’hui.
Par cette formulation, Newton ne réussit pas à expliquer la marée océanique côtière observée, mais définit une marée «statique» ou «d’équilibre».
C’est la marée formée par l’action d’un astre unique (ici la Lune) sur une Terre hypothétique recouverte entièrement (sans continents) d’une couche d’eau, sans inertie ni viscosité, représentant un océan de profondeur constante. Sur la verticale, l’équilibre est hydrostatique et le déplacement vertical maximum est de l’ordre de 55 cm pour l’action de la Lune (25 cm pour celle du Soleil). Quant à la pente de la surface océanique, elle induit un gradient horizontal de pression en équilibre avec la composante horizontale de la force génératrice.
Ainsi, la force d’attraction de la Lune sur toute particule à la surface du globe est donc toujours dirigée vers cet astre, mais d’intensité variable : cette dernière présente 2 maximums, le supérieur au zénith, point de la Terre le plus rapproché de la Lune et l’inférieur à l’opposé (nadir), mais l’écart de ces 2 maximums est très faible (du deuxième ordre).
Par contre, la force d’attraction lunaire au centre de masse de la Terre, dirigée également vers la Lune, a une intensité constante (égale en première approximation à la moyenne des deux extrêmes définies précédemment à la surface océanique, zénith et nadir). L’opposée de cette force peut être interprétée de nos jours comme la force centrifuge du centre de masse terrestre par rapport au repère barycentrique Terre-Lune (système à 2 corps), mais Newton n’utilisa pas cette appellation.
La force génératrice des marées est strictement verticale et dirigée vers le haut au zénith où la force d’attraction à la surface de l’océan est à son maximum, mais cette force génératrice est aussi dirigée vers le haut au nadir car, si l’attraction de l’océan (qui s’exerce vers la Lune, donc vers le centre de la Terre) tend à y faire baisser le niveau de la mer, la force d’attraction qui s’exerce au centre de masse de la Terre et qui est toujours constante, lui est supérieure en intensité et joue en sens inverse (tend donc au total à élever également le niveau de l’océan au nadir).
Dans ce schéma newtonien, du fait de la rotation terrestre, il y a donc nécessairement deux marées par jour en chaque point du globe. Newton eut bien conscience, contrairement à ses prédécesseurs, que l’on ne pouvait pas traiter séparément l’action de la Lune et celle du Soleil :
«Les deux mouvements que ces deux astres excitent, ne peuvent pas être aperçus chacun à part, mais il s’en compose un mouvement mixte».
Il expliqua le cycle des marées par les phases de la Lune, qui correspondent aux positions relatives de la Terre, de la Lune et du Soleil. Les marées de vives eaux surviennent lorsque le Soleil et la Lune sont en conjonction par rapport à la Terre (Nouvelle Lune) ou en opposition (Pleine Lune).
Les mortes eaux correspondent à une situation où les trois astres font un angle droit (quadrature), demi-lune montante ou descendante.
Newton mit ainsi, grâce à la gravitation universelle, un ordre physique dans le phénomène des marées. Mais son «modèle statique» appliqué à une planète complètement océanique, sans continents et de profondeur constante n’est pas réaliste. Comme déjà signalé plus haut, les calculs effectués à partir de la théorie statique débouchent sur des variations maximales de hauteur de 55 cm (pour la Lune) bien loin du marnage de 13 mètres de la baie du Mont Saint Michel. C’est normal puisque dans ce modèle statique, il n’y a pas la prise en compte de l’hydrodynamique (propagation des ondes) et de l’interaction océan-continent. Ce modèle est symétrique par rapport à l’axe Terre-Lune (thèse Lefèvre, 2000, fig.7), et la rotation terrestre (axe perpendiculaire à l’équateur, mais pas au plan orbital lunaire) impliquerait qu’en chaque point, il y ait deux marées par jour d’amplitudes inégales (inégalité diurne). Si l’équilibre statique était instantané, on ne devrait pas observer les retards qu’il y a entre la grande marée et la conjonction qui la produit, ou plus généralement entre la marée et le passage de la lune au méridien du lieu. On est encore loin des prévisions et des applications qui sont essentiellement côtières.
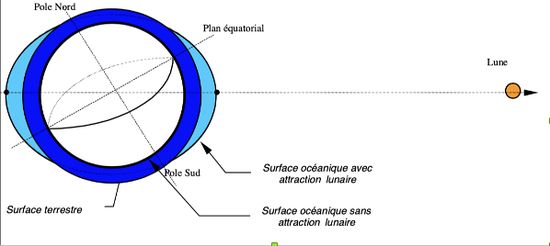
Thèse Lefèvre, 2000, fig.7
Laplace : le modèle dynamique
C’est Laplace, qui en 1775 introduit de la dynamique dans la marée et en fait un phénomène ondulatoire. La marée n’est plus un simple mouvement vertical de la surface en phase avec les mouvements de la Lune et du Soleil, ce sont des ondes qui se propagent dans l’océan.
Elles sont déviées par la force de Coriolis générée par la rotation de la Terre. Leur vitesse de propagation dépend de la profondeur qui est variable. Comme tout phénomène ondulatoire, elles sont réfléchies, réfractées et dissipées en fonction de la nature du milieu de propagation et de la forme des bassins océaniques. Elles se superposent, interfèrent entre elles, renforçant ou atténuant certaines périodes.
Il s’ensuit que la marée observée en un point, est le résultat de la superposition de toutes ces ondes élémentaires arrivant de tous les points de l’océan, en ayant rencontré chacune sur son trajet, des conditions de propagation différentes.
La marée peut être considérée comme la somme de composantes que l’on rattache aux variations périodiques des positions relatives Soleil-Lune-Terre.
Laplace définit ainsi le potentiel des marées en trois espèces qui dépendent de la configuration des trois astres concernés :
- espèce diurne (autour de 24 heures),
- espèce semi-diurne (environ 12 heures),
- espèce plus longue période.
À cette époque, les mesures de marée étaient faites à l’aide d’échelles de marée, simples règles graduée en bois placées verticalement, par exemple à l’entrée d’un bassin de radoub.
Les premières mesures en France furent faites à Brest en 1679 par les astronomes J.Picard et P. de La Hire. Elles furent systématisées à Brest à partir de 1711. C’est en utilisant les mesures faites entre 1711 et 1716 et en analysant les observations des hautes et basses mers à Brest que Laplace établit son modèle dynamique à trois espèces qui sera utilisé par le SHOM jusqu’en 1992.
C’est sur ces bases que le premier annuaire des marées fut publié en 1839 par l’ingénieur Hydrographe Rémi Chazallon: «Annuaire des marées des côtes de France». Le port principal était Brest où l’on appliquait la formule de Laplace et les dix ports secondaires y étaient rattachés par «concordance», c'est-à-dire que l’on établissait des relations empiriques entre les observations de Brest et les autres ports.
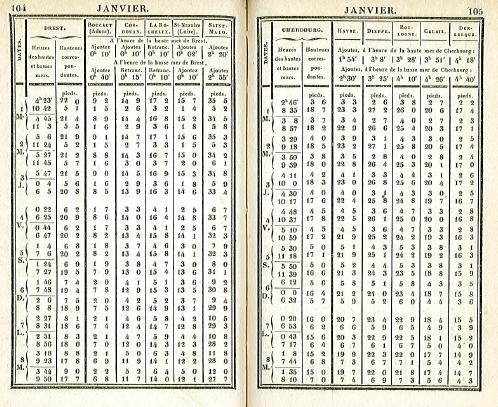
Extrait du premier annuaire des marées publié en France en 1839. Source SHOM
C’est le même Chazallon qui installera en 1846, à Brest toujours, le premier véritable «marégraphe» à enregistrement automatique à flotteur qui fonctionnera jusqu’en 1944, année où il fut détruit alors par les bombardements de la ville. Cette méthode dynamique fut utilisée en France jusqu’en 1992.
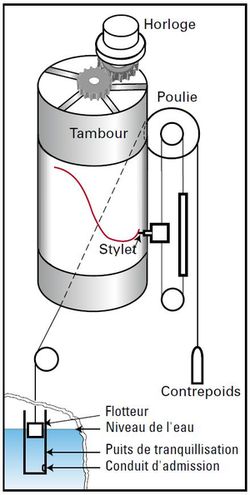
Marégraphe à flotteur - Source SHOM
L’analyse harmonique : la prévision opérationnelle
La méthode de Laplace est valable localement puisqu’elle part d’une analyse des mesures à un endroit donné (Brest), que l’on extrapole par «concordance» à d’autres ports. Pour généraliser la méthode, on ne peut se contenter des trois «espèces» de Laplace.
L’onde de marée est une superposition des très nombreuses composantes périodiques, directement liées au «potentiel de marées», qui dépend :
- exclusivement des influences «astrales»
- et de composantes non linéaires qui en dérivent,
générées par les interférences entre les ondes elles-mêmes et leurs interactions avec les continents.
Il était logique d’universaliser le potentiel des marées, en analysant à partir de mesures la totalité de ses composantes périodiques et en déterminant leur fréquence respective (analyse harmonique de Fourier). C’est ce que fit William Thomson, plus connu sous le nom de Lord Kelvin, en 1869. Il mit au point une machine «Tide Predictor», véritable machine à calculer mécanique faite de disques poulies, engrenages qui simulait les différentes composantes de marée et qui imprimait les courbes de marées prévues résultantes, sans avoir à les calculer, ce qui à l’époque eut été particulièrement fastidieux.
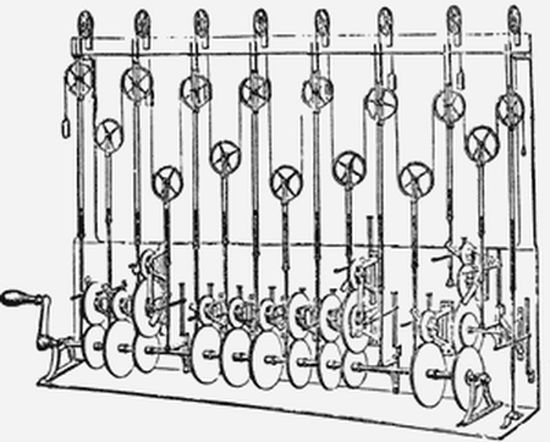
Tide predictor
La première machine de Kelvin (1873) intégrait 10 composantes, mais on passa rapidement à 40 composantes (Darwin 1883). Doodson poussa l’analyse en 1921 jusqu’à 388 composantes. Les machines les plus élaborées se contentèrent de 62 composantes. Le SHOM fit l’acquisition d’un Time Predictor en 1950 qui fonctionna pour l’outre-mer jusqu’en 1966.
Ces machines relayées par les ordinateurs sont maintenant des pièces de musée. En France, actuellement et depuis 1992, les prédictions de marée sont exclusvement calculées à l'aide de la méthode harmonique qui se base sur la représentation de la marée sous la forme d'une somme de 143 composantes périodiques. Ces composantes sont valables partout, ce qui permet d'élaborer des prédictions dans toutes les régions du monde quelque soit le type de marée que l’on y rencontre, du fait des différences de l’importance relative des divers composantes d’un endroit à un autre :
- semi-diurne,
- semi-diurne à inégalité diurne,
- mixte,
- diurne etc.
Ces prédictions sont calculées avec une précision de quelques centimètres pour les hauteurs et quelques minutes pour les heures. Cette maîtrise du phénomène des marées et de leur prévision aurait pu faire que l’histoire s’arrête là conceptuellement et concrètement, des progrès pouvant toujours être faits dans les observations et la modélisation. Ce ne fut pas le cas.
La marée et l’océanographie : conséquences des mesures satellitaires
La marée au large
La force des marées n’était, jusqu’à il n’y a guère, pas prise en compte lorsque l’on évoquait les moteurs de la circulation océanique, que l’on limitait à la force d’entraînement du vent et aux échanges thermodynamiques. La marée, pourtant génératrice, localement dans les régions côtières, de très forts courants, était perçue comme un phénomène bien maîtrisé parfaitement prévisible, réversible et à moyenne nulle. On en déduisait que l’influence de la marée sur la circulation générale océanique, celle des courants de surface comme des courants profonds était négligeable. Il n’en est rien et ce sont les techniques spatiales qui ont introduit l’énergie des marées comme acteur important de cette circulation océanique. Nous verrons plus loin comment les mesures de l’océan depuis les satellites ont «révolutionné» la recherche océanographique.
En 1992 fut lancé le satellite altimétrique franco-américain Topex/Poseidon. Son objectif était de mesurer avec une précision centimétrique les variations du niveau de la mer pour mesurer les courants marins. En effet les courants marins provoquent une dénivellation du niveau de la surface pouvant atteindre, par exemple dans le Gulf Stream, 1 m sur 100 km. Réciproquement, si l’on mesure cette variation, on peut en déduire la vitesse du courant. Mais la mesure satellitaire des variations du niveau de la mer inclut la marée et les courants qu’il faut séparer, soit que l’on s’intéresse à la marée, soit que l’on s’intéresse au courant. La précision des mesures, la couverture quasi-globale de l’océan effectuée par les satellites, la répétition des mesures sur de longues périodes ont permis d’améliorer la prévision des marées et surtout de résoudre la marée au large. Ainsi à partir du potentiel des marées, et dans la perspective de l’utilisation des données Topex/Poseidon pour l’étude des courants marins, Christian Le Provost a-t-il développé en 1994 le premier modèle global de marée de haute résolution. Il a servi, outre la prévision précise des marées au large, à bien calibrer les données du satellite afin qu’elles aient la qualité suffisante pour la mesure des courants océaniques.
La dissipation des marées et la circulation océanique
En arrivant sur les obstacles que constituent talus et plateaux continentaux, l’énergie de l’onde de marée contenue dans la masse d’eau va se transformer en énergie cinétique (les courants de marée que l’on utilise dans les usines marémotrices comme celle de la Rance) et en mélanges turbulents. C’est la «dissipation» de l’énergie des marées.
L’analogie peut-être faite avec la dissipation de l’énergie de la houle. Produite par le vent, elle ne concerne que les premières dizaines de mètres , et se propage en ondulant régulièrement au large, jusqu’à ce que frottant sur des petits fonds elle se cambre et déferle pour le plus grand plaisir des surfeurs.
Comparaison aussi avec les tsunamis : un séisme qui se traduit par un effondrement local du fond de l’océan produit une onde de masse océanique analogue à l’onde de marée. Elle se propage avec des vitesses comparables, et avec des amplitudes analogues au large, jusqu’à ce que, arrivant à la côte, son énergie se dissipe avec les effets dévastateurs que l’on sait.
La marée pourrait être vue comme un tsunami périodique dont la prévisibilité permet de s’y adapter. On a longtemps pensé que la quasi-totalité de la dissipation de l’énergie des marées, se faisait ainsi sur les talus et plateaux continentaux et qu’elle était négligeable en plein océan. C’était une erreur et l’on sait maintenant que 25 à 30% de la dissipation a lieu en plein océan et que la marée est un moteur essentiel de la circulation thermohaline, élément clé des transports de chaleur par l’océan des basses vers les hautes latitudes et donc de la dynamique du climat, le fameux tapis roulant qui sera décrit plus loin.
Le problème avait été posé au colloque de Williamstown - 1969, organisé en 1969 à l’instigation de la NASA, pour réfléchir aux projets spatiaux en vue d’une meilleure compréhension de la Planète Terre. Ce fut l’occasion d’une extraordinaire convergence entre astronomes et océanographes autour d’une question commune : qu’en est-il de la dissipation de l’énergie des marées ?
D’un côté les astronomes déduisaient la dissipation des marées (onde M2) :
- de l’éloignement de la Lune (3,8 cm/an),
- de son ralentissement
- du ralentissement de la rotation de la Terre
et l’évaluaient à 2,9x10*12 W.
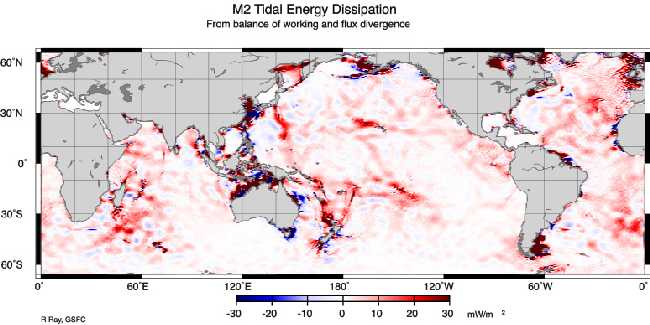
Dissipation de l’énergie de l’onde de marée M2 déduite de l’altimétrie.
De l’autre, les océanographes qui ne connaissaient que la dissipation sur les pentes et talus continentaux, l’estimaient entre 1,4 et 1,7x10*12 W, soit à peu près la moitié.
D’où le problème de "l’énergie manquante" dont avaient besoin, à la fois les astronomes et les océanographes, pour boucler le bilan énergétique de la circulation thermohaline, qui implique de l’énergie pour expliquer la remontée vers la surface d’eaux venant des profondeurs. En 1996 lors d’une réunion du «Scientific Working Team» de Topex/Poseidon, Christian Le Provost apporta une contribution décisive en faisant la première évaluation à partir d’un modèle hydrodynamique des marées (Le Provost et Lyard 1997).
La confirmation expérimentale est venue de l’espace et de la mesure du niveau de la mer par le satellite altimétrique Topex/poseidon. L’océan a un fond. Dans leur propagation, les ondes de marée perdent de l’énergie par frottement sur le fond des océans. Énergie transformée en mélange turbulent qui fait que les couches les plus profondes, donc les plus denses, se mélangent avec les couches d’eaux plus légères qui les surmontent, ce qui revient à faire remonter progressivement par mélange les eaux de fond.
Les fonds océaniques ne sont pas plats, ils sont parcourus de chaînes montagneuses (les dorsales médio-océaniques) et parsemés de monts sous marins qui peuvent surplomber les plaines abyssales de deux à trois mille mètres. Autant d’obstacles formidables sur lesquels viennent buter les ondes de marée qui vont y dissiper une partie importante de leur énergie, et induire des mélanges turbulents qui feront que progressivement et de manière diffuse en différents endroits de l’océan, les eaux profondes se rapprocheront de la surface où le vent les réintégrera dans la circulation océanique de surface pour un nouveau voyage !
La dissipation de l'énergie (qui est en fait une transformation d'énergie), se fait au sein du fluide par l’intermédiaire d'ondes dites "ondes internes" qui, faisant varier lors de leur passage la structure verticale de densité, ont une influence sur l'élévation du niveau de la mer. Influence faible : variation de l’ordre du cm du niveau de la mer. Variation suffisante pour être détectée par Topex/Poseidon qui permit ainsi d’évaluer cette énergie dissipée et d’en localiser les principaux points dans l’océan et de rassurer océanographes et astronomes ! La marée affirma ainsi son droit à être pleinement prise en compte dans l’océanographie.
Une video intéressante à visualiser
Cette vidéo est une animation issue de la modélisation réalisée par Christian Le Prosvost et son équipe en 1999 (s’appuyant sur les mesures altimétriques du satellite altimétrique Topex-Poseïdon), pour deux des composantes lunaires majeures définies par George Darwin : l’onde semi-diurne M2 dont la période est de 12h25mn et l’onde diurne K1 (due à l’inclinaison de l’orbite lunaire par rapport à l’équateur) dont la période est égale au jour sidéral (23h56mn).
Pour la compréhension de cette vidéo, il convient de rappeler que pour chaque composante de marée, la latitude critique est la latitude où la période de Coriolis est égale à la période de cette composante. Ces latitudes interviennent dans le processus de dissipation de la marée par les ondes internes engendrées par ces différentes composantes. Pour l’onde K1, cette latitude est proche de 30° dans chaque hémisphère.
Voir aussi FAQ :
Qu'en est-il de la dissipation de l'énergie des marées? Quel rôle joue-t-elle dans la circulation thermohaline? Bruno Voituriez - mars 2008.
Mis à jour mars 2020

