Les hydroliennes
Jacques Ruer
I - Principe
II - Ressource énergétique des courants de marées
III - Conversion de l’énergie cinétique du courant
IV - Contrôle de la puissance − cas d’une hydrolienne avec rotor-hélices
V - Production énergétique d’une hydrolienne
VI - Cavitation
VII - Influence de l’orientation relative du rotor avec le courant
VIII - Types d’hydroliennes
VIII - 1 Rotor à axe horizontal
VIII - 2 Rotor à flux transverse
VIII - 3 Capteurs oscillants
I - Principe
Une hydrolienne est une machine hydraulique qui exploite l’énergie cinétique de la masse d’eau environnante. Elle peut être comparée à une éolienne sous-marine produisant de l’électricité à partir du courant d’eau.
II - Ressource énergétique des courants de marée
On verra au paragraphe suivant que seuls les courants ayant une vitesse maximale supérieure à 2 m/s, voire 2,5 m/s présentent un intérêt pour l’implantation d’hydroliennes. En mer, on observe des courants périodiques induits par la marée, ainsi que des courants océaniques qui sont relativement stables.
Les courants de marée sont importants dans les régions où le marnage est important, dans les zones où la configuration de la côte oblige la masse d’eau à accélérer.

Figure 1 : Carte des vitesses maximales des courants de marée dans la Manche. Les courants sont rapides là où la masse d’eau entrainée par l’onde de marée doit contourner des pointes, ou des îles et passer au dessus d’un haut-fond – Source : SHOM
Les sites présentant des courants rapides sont très localisés, comme on peut le voir sur l’exemple de la figure 1. La profondeur d’eau est toujours inférieure à 50 m. Les sites sont situés à une distance assez faible de la côte, ce qui simplifie le raccordement électrique.
À titre d’exemple, lors d’une marée de vive-eau, la vitesse maximale du courant atteint m/s entre Aurigny et la Pointe de la Hague (Raz Blanchard). La vitesse maximale est quasiment proportionnelle à l’amplitude de la marée, donc au coefficient de marée.

Figure 2 : Vitesses du courant dans l’archipel de Molène et autour d’Ouessant 3 h après la pleine mer de Brest lors d’une marée de coefficient 103 – La carte représente une zone de 37km x 56km − Source : Previmer.org
La ressource théorique de l’énergie des courants de marée sur les côtes françaises est estimée à 6 000 MW. La ressource accessible en tenant compte des contraintes économiques et réglementaires est probablement la moitié de cette valeur.
En comparaison, les courants océaniques sont nettement moins rapides. Les figures 3 et 4 montrent la vitesse moyenne du Gulf Stream dans le détroit de Floride, à l'endroit où ce courant le plus rapide au monde atteint sa plus grande vitesse. On constate que la vitesse maximale est d’environ 1,8 m/s, ce qui est nettement moins rapide que les courants de marée dans les sites propices.
 cm s-1
cm s-1
Figure 3 : Carte des vitesses du Gulf Stream et de la dérive Nord-Atlantique - Source : Cooperative Institute for Marine & Atmospheric Studies

Figure 4: Vitesse dans le détroit de Floride − La vitesse est maximale près de la côte de Floride en surface et beaucoup plus faible près de la côte cubaine
III - Conversion de l’énergie cinétique du courant
Considérons une hydrolienne avec un rotor de diamètre D immergé dans un courant dont la vitesse est V.

Figure 5: Schéma du courant agissant sur une hydrolienne
La surface du rotor est : S = п/4.D2
La masse d’eau qui traverse le rotor à chaque seconde est : M= ρ.S.V ρ : masse volumique du fluide
L’énergie cinétique de cette masse d’eau est : E = ½ M.V2 = ½.ρ.S.V3*
La puissance de l’hydrolienne est une fraction de l’énergie cinétique:P = Cp.E avec Cp : coefficient de performance de l’hydrolienne.
On obtient : P = ½.Cp.ρ.S.V3 (1)
Le coefficient de performance Cp dépend de la qualité de réalisation du capteur d’énergie, par exemple le rotor de l’hydrolienne. On démontre (théorie de Betz) que dans une profondeur d’eau infinie, Cp est égal au maximum à la limite de Betz : 16/27 = 0,59. Cette théorie est fréquemment utilisée pour les éoliennes. Sans prétendre expliquer ici cette théorie, il suffit de considérer que le fluide qui entre dans le rotor d’un coté, doit en ressortir de l’autre coté. Le fluide sortant possède une vitesse non nulle, donc une énergie cinétique résiduelle qui n’a pas été soustraite par le rotor.
En fait, dans le cas des hydroliennes, la profondeur d’eau n’est pas infinie, si bien que la théorie doit être révisée. La théorie détaillée sort du cadre de cette présentation.
Les rotors réels des hydroliennes ont un Cp voisin de 0,40 à 0,45.
La figure 6 montre la relation entre la vitesse du courant et la puissance électrique pour une hydrolienne de 200 kW. Lorsque le courant est plus rapide que la vitesse nominale prise en compte pour le dimensionnement de la machine, la puissance est bridée à la valeur maximale. Ceci résulte du fait que le raccordement électrique est prévu pour une puissance donnée, qu’il n’est pas possible de dépasser.

Figure 6: Relation entre la vitesse du courant et la puissance pour une hydrolienne théorique de 200 kW dessinée pour délivrer sa puissance maximale pour un courant de 2,5 m/s − Lorsque le courant est inférieur à la vitesse nominale, la puissance varie selon le cube de la vitesse ; pour des vitesses supérieures, l’hydrolienne est pilotée pour maintenir la puissance électrique constante.
Le fait que la puissance soit proportionnelle au cube de la vitesse du courant entraine beaucoup de conséquences dans la conception des hydroliennes et la sélection des sites propices à l’exploitation de cette forme d’énergie.
Imaginons pour fixer les idées, qu’on désire obtenir une puissance électrique de 200 kW grâce à une hydrolienne. Le tableau suivant indique en fonction de la vitesse maximale du courant sur divers sites potentiels le diamètre du rotor.
Le tableau indique ce que seraient les données pour une éolienne ayant la même puissance.
Le tableau indique aussi la force qui s’exerce sur le rotor de l’hydrolienne. Elle est donnée par la formule :
F = ½. Cf.ρ.S.V2 (2)
Tableau 1 : Dimensions d’une hydrolienne de 200 kW en fonction de la vitesse du courant prise en compte pour le dimensionnement − Cp = 0,40 − Cf = 1,0
| Vitesse maximale du courant sur le site | Surface de captation du flux | Diamètre rotor circulaire | Poussée horizontale théorique |
| 4 m/s | 15,3 m2 | 4,4 m | 125 kN |
| 3 m/s | 36,2 m2 | 6,8 m | 167 kN |
| 2 m/s | 122,1 m2 | 12,5 m | 250 kN |
| 1,4 m/s | 355,9 m2 | 21,3 m | 357 kN |
| 1 m/s | 976,6 m2 | 35,3 m | 500 kN |
| Éolienne : vent de 13 m/s | 352,8 m2 | 21,2 m | 42 kN |
On constate que l’hydrolienne a une taille plus faible que l’éolienne de même puissance si le courant local est rapide. Sinon, c’est l’inverse. On lit fréquemment sur internet des annonces concernant l’invention de nouvelles hydroliennes capables d’exploiter les courants de faible vitesse. Le tableau ci-dessus montre que cet espoir n’est économiquement pas viable. Soulignons que ce tableau est calculé à partir de considérations sur l’hydrodynamique du fluide, et que la technologie mise en œuvre n’intervient pas dans le calcul, que le rotor soit une hélice à flux axial, à flux transverse ou une membrane ondulante.
On constate aussi que la poussée horizontale est d’autant plus forte que la vitesse du courant est faible.
IV - Contrôle de la puissance – cas d’une hydrolienne avec rotor-hélice
La vitesse du courant est parfois inférieure à la vitesse nominale, parfois supérieure lors des grands coefficients de marée. Afin d’illustrer la manière dont il est possible de contrôler la puissance, considérons le cas d’une hydrolienne mécaniquement très simple, munie d’un rotor en forme d’hélice avec des pales non réglables, placée perpendiculairement au courant. La figure 7 montre que la puissance délivrée varie en fonction de la vitesse de l’eau, mais aussi de la vitesse de rotation. La puissance passe par un maximum quand la vitesse de rotation augmente, puis s’annule pour la vitesse dite de roue libre. La vitesse de roue libre est proportionnelle à celle de l’eau, si bien que la valeur du maximum de puissance suit une loi cubique similaire à la formule (1).

Figure 7 : Caractéristiques de puissance d’une hydrolienne munie d’un rotor en forme d’hélice en fonction de la vitesse du courant et de la vitesse de rotation — La puissance nominale est de 450 kW pour un courant de 3 m/s — La courbe 0-A-B représente la puissance fournie par une génératrice conçue pour délivrer 450kW au maximum – La partie 0-A est située légèrement à droite de la courbe des lieux du maximum de puissance pour des raisons de stabilité — (voir texte)
Lorsque la vitesse de l’eau est inférieure à la vitesse nominale (ici 3,0 m/s), la puissance varie comme le cube de la vitesse du courant. Le système électronique qui contrôle la génératrice doit régler la puissance produite en fonction de la vitesse de rotation d’une manière convenable. Supposons en effet que pour un courant de 2,5 m/s, on désire obtenir la puissance maximale théorique, égale dans ce cas à 300 kW, atteinte pour une vitesse de rotation de 13 rotations par minute (13 rpm). Un léger dérèglement risque de faire baisser la vitesse du rotor en dessous de cette vitesse optimale.
On voit sur la figure 7 que si la vitesse tombe en dessous de 13 rpm, la puissance hydraulique du rotor diminue, si bien que la vitesse de rotation ralentit ; la puissance diminue encore, la vitesse baisse à nouveau, ainsi de suite jusqu’à l’arrêt complet. On parle de décrochage.
Il est préférable de régler le système pour que la vitesse de rotation pour un courant de 2,5 m/s soit de 15 rpm, avec une puissance fournie à la génératrice de 250 kW. Grâce à cette disposition, une légère baisse de la vitesse de rotation conduit à une augmentation de la puissance hydraulique. Celle-ci est alors supérieure à la puissance extraite par la génératrice. La différence accélère le rotor qui revient à la vitesse normale de 15 rpm. À l’inverse, une accélération fortuite et passagère de la vitesse de rotation se traduit par une baisse de la puissance hydraulique. Le rotor est automatiquement freiné par la génératrice et revient à la vitesse initiale.
Lorsque le courant de marée a une vitesse supérieure à la vitesse nominale de 3 m/s, le rotor tourne plus vite que 15 rpm, mais il est possible électroniquement de ne pas laisser la génératrice produire plus que la puissance désirée de 450 kW.
En résumé, sur la figure 7, la zone située à droite de la courbe des maxima correspond à un fonctionnement stable, tandis que celle située à gauche est instable.
La figure 8 schématise la chaine électrique d’une hydrolienne équipée d’une génératrice à aimants permanents.

Figure 8 : Schéma simplifié de l’architecture électrique d’une hydrolienne à aimants permanents
La génératrice fournit un courant dont la fréquence varie avec la vitesse de l’eau. Ce courant alternatif est d’abord transformé en courant continu grâce à un étage de conversion électronique équipé de transistors de puissance, dits transistors bipolaires à grille isolée (en anglais : IGBT). L’énergie électrique sous forme de courant continu peut être stockée dans des super-condensateurs afin de lisser les fluctuations de puissance dues par exemple à l’action de la houle (voir figure 12 ci-après).
Le courant continu est ensuite transformé en courant alternatif triphasé 50 Hz, en phase avec le réseau de transport continental pour permettre l’exportation de l’énergie. Un transformateur à rapport de tension réglable permet d’ajuster la tension de sortie à celle du réseau.
On constate que la technologie moderne de l’électronique de puissance permet maintenant de concevoir des hydroliennes dont l’architecture mécanique est simple. Les fonctions sophistiquées permettant d’accommoder les variations de puissance sont obtenues par des moyens électroniques et non par des moyens mécaniques (par exemple pales réglables à incidence variable). La fiabilité de l’ensemble est améliorée.
V - Production énergétique d’une hydrolienne
Comme la vitesse du courant est proportionnelle à l’amplitude de la marée, la formule (1) montre que la puissance varie énormément d’une heure à l’autre et d’un jour à l’autre en fonction du coefficient de marée.
Pour illustrer la variation de la production d’énergie selon les jours, on considère un exemple théorique, avec une hydrolienne de 500 kW implantée dans un site typique de la Manche. La figure 9 montre la vitesse du courant sur ce site durant le mois d’octobre 2008.

Figure 9: Vitesse du courant entre le 01/10/2008 et le 31/10/2008
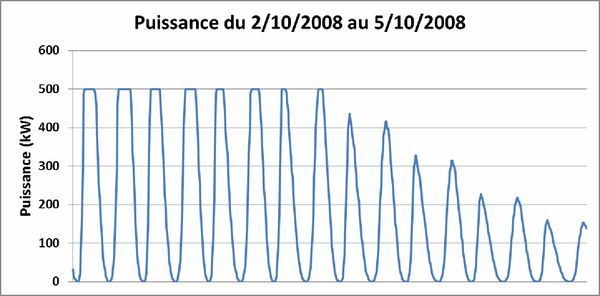
Figure 10 : Production durant une période de vive-eau — La puissance nominale est atteinte les 2 et 3 octobre — Les coefficients de marée sont trop faibles à partir du 4 octobre

Figure 11: Production durant une période de morte-eau
Le calcul de la production cumulée pour ce site pour toute l’année 2008 montre que l’hydrolienne aurait pu fournir un total de 1 516 073 kWh.
En divisant cette quantité par la puissance nominale de l’hydrolienne, on obtient :
1516073 kWh / 500 kW = 3032 h
Ce nombre d’heures constitue ce qu’on nomme la durée équivalente de fonctionnement pleine puissance.
Si on divise l’énergie par le nombre d’heures dans une année (8760 h), on obtient la puissance moyenne :
1 516 073 kWh / 8760 h = 173 kW
Le ratio 173 kW / 500 kW = 0,35 est nommé facteur de charge.
Ces valeurs sont similaires à celles obtenues quand on effectue les calculs pour une éolienne dans un site bien venté. L’énergie hydrolienne présente donc un facteur de charge similaire à l’éolien. Elle possède toutefois un avantage important : l’énergie des courants de marée est prévisible très longtemps à l’avance.
En mer ouverte, la houle se superpose au courant de marée. La combinaison des vitesses du courant et du mouvement cyclique induit une fluctuation de la puissance instantanée, comme on peut le voir sur la figure 12. Pour s’affranchir de cette influence, on peut stocker temporairement les surplus d’énergie grâce à des batteries ou des super-condensateurs (voir figure 8).

Figure 12 : Mesures de la vitesse instantanée du courant et de la puissance de l’hydrolienne — On note les variations dues à l’influence d’une forte houle lors de la mesure — Projet SEAFLOW Marine Current Turbines
VI - Cavitation
L’analogie avec les éoliennes connaît une limite à cause du phénomène de cavitation. L’eau qui circule à proximité d’une aile subit des différences de pression. Une surpression existe sous la face d’intrados, tandis qu’une dépression est présente sur l’extrados (voir figure 13). Or, si la pression locale devient inférieure à la pression pour laquelle l’eau s’évapore, des bulles de vapeur se forment.

Figure 13: Schéma du phénomène de cavitation

Figure 14 : Maquette de rotor d’hydrolienne dans un canal d’essai — Les zones brillantes à l’extrémité des pales sont les bulles de cavitation — À l’extrémité des pales, les tourbillons provoque le dégazage d’air dissous. Les chapelets de bulles visualisent la trace en hélice du passage des extrémités des pales dans l’eau.
La cavitation est gênante, car les bulles implosent dès que la pression ambiante remonte, en dehors de la zone de formation. Lorsque les bulles sont en contact avec la paroi, l’implosion provoque une onde de choc locale capable d’éroder la surface, ce qui conduit à une usure prématurée du matériel.

Figure 15 : Hélices de navire montrant des zones érodées par la cavitation.
Un moyen simple d’éviter la cavitation consiste à limiter la vitesse tangentielle en extrémité de pale. La dépression sur l’extrados est proportionnelle à l’énergie cinétique du fluide :
Δ P = ½ k.ρ.V2 (3)
Le facteur k dépend du profil de l’aile et d’autres facteurs.
La cavitation apparaît si :
P = ρ.g.z – Δ P < Pvap (4)
La pression de vapeur saturante Pvap ne dépend que de la température. Elle est très faible à la température ordinaire, par exemple 1,7 kPa à 15 °C, à comparer avec la pression atmosphérique qui est de 101 kPa.
La formule (4) montre que la cavitation dépend de la profondeur (z) et de la vitesse de la pale (V).
VII - Influence de l’orientation relative du rotor avec le courant
On pourrait penser qu’il est important de conserver en permanence l’axe du rotor dans celui du courant, car l’orientation précise du courant varie au fil des heures.
La figure 16 montre la rose des courants en divers points de la côte Bretagne-Cotentin, ce qui permet d’estimer la perte d’énergie dans le cas où le rotor est fixe dans l’espace, alors que la direction du courant est variable.

Figure 16 : Roses de courant en divers points de la côte Bretagne-Cotentin — Chaque diagramme local indique la variation de l’orientation et de la vitesse du courant au fil des heures — Le courant est essentiellement parallèle à la côte — Le site des Minguiers présente une rose elliptique − Source : SHOM.
On constate que les courants sont parallèles à la côte, dans un sens ou dans l’autre selon l’heure. Sur le site des Minguiers situé entre Jersey et Bréhat, la rose présente une forme elliptique, le courant transverse ayant une vitesse environ égale au tiers du courant maximal axial. Si on considère de nouveau la formule (1), on arrive à la conclusion que la puissance de ce courant transverse n’est que 4 % de la puissance maximale lorsque le courant est aligné avec le grand axe de l’ellipse. Ceci montre que même sur un site de ce genre, il n’est pas judicieux de s’efforcer d’orienter le rotor à tout instant. Un rotor fixe est quasiment aussi efficace qu’un rotor orientable.
VIII - Types d’hydroliennes
Lors de la conception d’une hydrolienne, plusieurs paramètres s’offrent au choix de l’ingénieur. Il est ainsi possible d’imaginer de nombreuses machines d’aspects fort différents. On décrit dans ce qui suit les principaux types de capteur destinés à transformer l’énergie cinétique de l’eau en énergie mécanique utilisable. Quelques exemples sont présentés ensuite, en tentant de montrer la démarche qui a conduit la conception dans chaque cas.
VIII - 1 Rotor à axe horizontal
Le rotor est une hélice placée perpendiculairement au courant. Ce genre d’hydrolienne est similaire à une éolienne qui tournerait dans l’eau.

Figure 17 : Schéma d’une hydrolienne équipée d’un rotor hélice perpendiculaire au courant.
La théorie des hélices enseigne que les pales du rotor se comportent comme des ailes qui interagissent avec le fluide à proximité (tourbillons de Joukowski). La figure 18 montre que lorsque le rotor tourne, les pales tracent dans le fluide des hélices entrelacées, si bien que l’ensemble de l’eau qui traverse le rotor interagit avec au moins une des pales. La vitesse de rotation est inversement proportionnelle au nombre de pales. Moins il y a de pales, plus la vitesse doit être élevée afin qu’aucune particule d’eau ne puisse traverser le rotor sans subir l’influence d’au moins une pale.

Figure 18 : Visualisation des tourbillons liés aux pales du rotor — Les pales tracent dans l’eau des hélices étroitement entrelacées Seuls les tourbillons d’extrémité des pales sont figurés pour la clarté de l’image — Le flux en aval du rotor est plus large qu’à l’amont car la vitesse aval est plus basse — On voit que certaines lignes de flux aval ont acquis une composante de vitesse tourbillonnaire, celle-ci est toutefois réduite, le flux aval reste essentiellement axial — Source : Oxford Energy.
Hélices carénées
Certaines hydroliennes qui utilisent le principe du rotor-hélice sont munies d’un carénage. La forme interne du carénage dessine un venturi convergent-divergent. La vitesse de l’eau au droit du rotor est supérieure à la vitesse environnante. Les promoteurs de la technique du rotor caréné insistent sur le fait que le diamètre de l’hélice est alors plus faible que pour un rotor libre, ce qui est exact. Toutefois, la puissance captée est dictée par le diamètre de l’entrée du convergent. On peut démontrer que cette puissance est identique à celle obtenue avec un rotor libre dont le diamètre serait égal au diamètre d’entrée (figure 19).
Du point de vue économique, le coût du carénage dépasse largement l’économie faite sur le rotor proprement dit. De plus, si l’hydrolienne est implantée dans un site ouvert à l’influence de la houle, le carénage de grande dimension est soumis à de gros efforts hydrodynamiques qui obligent à augmenter la résistance mécanique de la structure et le coût des ancrages.


Figure 19 : Comparaison d’un rotor caréné et d’un rotor libre — La puissance captée est identique si les diamètres D sont égaux.
Le principe du rotor hélice est utilisé dans de nombreux types d’hydrolienne. On ne citera ici que quelques exemples représentatifs.
Sabella
L’hydrolienne est conçue dans un esprit de simplicité, avec le minimum possible d’éléments mobiles. Elle est posée sur le fond afin de se soustraire autant que possible à l’action des vagues, car les sites visés (par exemple Ouessant) sont situés en mer ouverte et balayés par les tempêtes.
La nacelle est posée sur un tripode lesté. L’hydrolienne est fixe dans l’espace. L’ensemble est orienté lors de l’installation en tenant compte d’un compromis entre la direction du courant lors du flot et du jusant.
Les pales sont fixées rigidement au moyeu. Le sens de rotation du rotor s’inverse avec le sens du courant. Les pales sont symétriques, car chaque face des ailes est alternativement extrados puis intrados. Ce type de profil est un compromis qui n’est pas optimum du point de vue rendement. Ceci est aisément compensé en donnant au rotor un diamètre légèrement plus grand (+5%) que celui d’un rotor théorique qui serait muni de pales optimales. Pour éviter la cavitation, le rotor tourne assez lentement et comporte 6 pales.
On ne peut pas faire varier l’incidence des ailes. Par conséquent, la vitesse de rotation est variable, proportionnelle à la vitesse de l’eau. La génératrice est couplée directement au rotor, sans engrenages intermédiaires, ce qui augmente la fiabilité. Le courant électrique variable produit par la génératrice est transformé en courant triphasé 50 Hz grâce à des convertisseurs électroniques convenables (Voir figure 8).
L’idée fondamentale de la conception est que la simplification mécanique doit permettre de minimiser les risques de panne et les besoins de maintenance.

Figure 20 : Vue de l’hydrolienne Sabella D10 lors de son installation — La nacelle est montée sur un socle tripode soigneusement lesté pour maintenir l’ensemble en position même lors des tempêtes — Source : Sabella SAS
Hydrolienne OpenHydro
L’hydrolienne comporte un carénage circonscrit au rotor. La présence du carénage améliore l’uniformité du flux sur le rotor. On voit sur la figure 21 que les pales sont fixées sur un anneau qui roule dans une gorge aménagée dans la surface interne du carénage. L’anneau porte les aimants permanents de la génératrice, tandis que les bobinages du stator sont intégrés dans le carénage. Dans cette conception, la génératrice fonctionne complètement immergée dans l’eau. Il ne peut donc pas y avoir de problème lié à une perte d’étanchéité. Par contre, la nécessité de maintenir l’isolation électrique des bobinages conduit à un grand entrefer entre les faces magnétiques des aimants permanents portés par l’anneau mobile et les bobinages du stator. La friction de l’eau emprisonnée dans l’entrefer lorsque l’anneau tourne engendre une perte d’énergie dont il faut tenir compte dans le calcul du rendement.
L’électricité produite a une fréquence variable, en fonction de la vitesse du courant de marée. Des équipements électroniques intermédiaires permettent d’élaborer le courant aux caractéristiques exigées par le réseau.
Des éléments mécaniques doivent assurer le centrage précis du rotor dans le carénage et compenser la poussée hydrodynamique axiale.
La présence du carénage augmente les efforts dus aux vagues lors des tempêtes. Le lestage de l’ensemble doit être prévu en conséquence.

Figure 21 : Vue d’une hydrolienne OpenHydro sur sa barge d’installation — On voit les pales fixées sur un anneau mobile inséré dans un carénage — Le centre du rotor est vide — Source : DCNS
Hydrolienne Oceade
Cette hydrolienne est très semblable à une éolienne sous-marine, comme on peut s’en rendre compte sur la figure 22.
Le rotor est positionné face au courant. La nacelle pivote lors de la renverse grâce à un propulseur auxiliaire. Les pales ont une incidence réglable à volonté. Les pales du rotor peuvent avoir un profil optimal offrant la meilleure efficacité hydrodynamique.
La nacelle peut être amenée sur le site en flottaison, grâce à un remorqueur modeste (Voir figure 23). Le support tripode est apporté par un navire de travail, mais n’a pas besoin d’être relevé lors des opérations de maintenance. Durant le remorquage en surface, les pales doivent être orientées de façon à minimiser la trainée et éviter que la nacelle ne tourne. La facilité relative de l’installation de la nacelle permet d’intégrer dans celle-ci des équipements sophistiqués, notamment un multiplicateur de vitesse à engrenages. Comme la vitesse de rotation de la génératrice est grande, la taille de celle-ci est nettement plus faible que pour une génératrice tournant à la vitesse du rotor.

Figure 22 : Hydrolienne Oceade — Source : Alstom

Figure 23 : Remorquage de la nacelle d’un hydrolienne Oceade-2 des 3 pales restent immergées, elles doivent être « mises en drapeau » pour que le convoi puisse garder un cap et que la nacelle ne bascule pas — Le tripode support reste en place sur le fond — Source : Alstom
Hydroliennes flottantes
De nombreux modèles d’hydrolienne flottante ont été et continuent à être inventés et testés. La conception est guidée par le désir de faciliter l’installation et la maintenance.

Figure 24 : Schéma d’un hydrolienne flottante munie d’un rotor-hélice. Le flotteur est amarré sur le fond — Le rotor peut être sorti de l’eau pour la maintenance et le remorquage
L’hydrolienne est constituée d’un flotteur amarré sur le fond. La trainée du rotor provoque une traction sur l’ancrage, et le flotteur doit avoir une flottabilité suffisante pour ne pas être entrainé sous la surface par la traction de l’ancrage. Un flotteur en surface est sensible aux vagues, si bien que ce type d’hydrolienne ne convient guère que pour les sites relativement abrités de la houle du large.
Ces machines sont en surface, ce qui implique que leur présence visible soit acceptée du voisinage, et qu’elles ne constituent pas une gêne pour la navigation.
Un exemple est fourni par l’hydrolienne développée par Scotrenewables.
Le flotteur porte 2 rotors placés au bout de bras articulés. Les 2 rotors tournent en sens inverse afin de ne pas engendrer de mouvement latéral.
Durant le remorquage, mais aussi en cas de tempête, les bras sont repliés. Pour minimiser la trainée durant cette phase, chaque rotor ne peut comporter que 2 pales, qui viennent se ranger sous le flotteur. Le faible nombre de pales par rotor oblige à soigner le profil des ailes pour éviter la cavitation. Un tel profil est non symétrique, si bien que l’hydrolienne doit pivoter lors de la renverse pour toujours faire face au courant.


Figure 25 : Hydrolienne flottante Scotrenewables — En position opérationnelle, les bras portant les rotors sont déployés sous le flotteur — En position remorquage ou survie, les rotors sont repliés — L’hydrolienne doit pivoter autour de son point d’ancrage lors de la renverse — Source : Scotrenewables
VIII.2 - Rotor à flux transverse
Ce type de capteur diffère de l’hélice, car les pales tournent autour d’un axe perpendiculaire au courant. Il est hérité des éoliennes Darrieus.
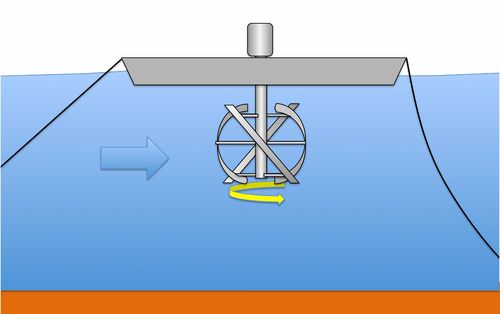
Figure 26 : Schéma d’une hydrolienne à flux transverse — Dans cette figure, l’hydrolienne est flottante, mais certains modèles sont posés sur le fond — On voit ici un avantage du rotor à axe vertical pour une hydrolienne flottante : la génératrice est hors de l’eau, sur le flotteur
Un rotor à flux transverse comporte plusieurs pales qui coupent le flux du courant 2 fois à chaque tour. La figure 27 montre que les pales sont accompagnées de tourbillons qui correspondent à l’apparition des forces hydrodynamiques, tantôt d’un côté du profil, tantôt de l’autre, de façon alternée. Ces tourbillons se détachent pour certaines valeurs de l’angle de rotation du rotor, avec une annulation soudaine puis une inversion du sens des forces sur la pale. Ce comportement est donc très différent de celui d’une hélice conventionnelle pour laquelle les tourbillons de Joukowski restent attachés aux pales. Le rendement effectif d’un rotor à flux transverse est inférieur à celui d’un rotor-hélice.

Figure 27 : Simulation numérique de l’écoulement dans un rotor à flux transverse — On voit 3 pales profilées qui tournent autour d’un axe dans le sens inverse des aiguilles d’une montre (sens antihoraire) — Les tourbillons bleus tournent dans le sens horaire, les rouges dans le sens antihoraire — À chaque tour, une pale forme un tourbillon dans un sens qui se détache brutalement, puis un autre dans le sens contraire qui se détache à son tour, etc. — Les tourbillons détachés sont emportés par le courant — Voir l’animation youtube
Si les pales sont verticales, l’inversion des forces se produit instantanément sur toute la pale, ce qui peut engendrer des vibrations et une fatigue prématurée. Le rotor doit être construit très rigide (voir exemple figure 28).

Figure 28 : Vue d’une hydrolienne avec 6 rotors transverses — L’hydrolienne comporte 2 axes verticaux tournant en sens inverse, portant chacun 3 rotors à pales verticales (visibles en jaune). Les 3 rotors sont décalés angulairement pour atténuer les variations d’effort — Notez le carénage et la structure (en vert) qui porte des paliers intermédiaires ce qui minimise les déformations des arbres — Source : CMN-Hydroquest
Une autre solution consiste à donner aux pales une forme en hélice. Le largage des tourbillons se produit progressivement le long de la pale, au fur et à mesure que l’angle de rotation critique est atteint, sans créer de vibration.

Figure 29 : Alexander M. Gorlov montrant la turbine à axe vertical qui porte son nom, munie de pales hélicoïdales
Rotor transverse à axe horizontal

Figure 30 : Hydrolienne à rotors transverses tournant autour d’un axe horizontal — La structure porte des paliers intermédiaires — Ces hydroliennes sont destinées aux sites ayant une faible profondeur d’eau — Source : RivGen
VIII.3- Capteurs oscillants
De nombreux autres modèles d’hydrolienne ont été inventés. On peut citer ici les hydroliennes avec aileron oscillant ou membrane ondulante. Ces dispositifs s’inspirent du mouvement des nageoires des poissons.

Figure 31 : Schémas d’hydroliennes avec capteurs oscillants, à aileron ou à membrane ondulante
De manière générique dans cette famille de capteurs, l’énergie est captée par une surface qui décrit un mouvement alternatif perpendiculaire au courant. Chaque oscillation fait apparaître une force qui est exploitée. La production d’énergie est non constante et s’annule 2 fois par cycle. Un stockage d’énergie de courte durée est obligatoire.
Le sillage aval constitue une allée de Von Karman, formée de tourbillons alternés. Le flux de courant qui interfère avec le capteur est délimité par la largeur de cette allée. La fréquence optimale d’oscillation est déduite de la formule :
F(Hz) = 0,2.V/H (5)

Figure 32 : Schéma d’un capteur oscillant avec une allée tourbillonnaire de Von Karman dans le sillage
Pour aller plus loin
(1) Modèlisation et analyse pour la Recherche Côtière - Ifremer.
(2) Sabella
(3) Oceade
(4) ScotRenewables
(6) Tidal Stream
